Các công thức, hệ thức lượng trong tam giác vuông đầy đủ

Bài viết dưới đây được chia sẻ từ THPT CHUYÊN LAM SƠN sẽ giúp bạn hiểu hơn về các công thức hệ thức lượng trong tam giác vuông, mọi người đón xem để có thể hiểu hơn các hệ thức lượng trong tam giác vuông để áp dụng giải bài tập.

=> Mời bạn đón đọc các công thức đạo hàm chi tiết đầy đủ nhất

Định lí : Trong tam giác vuông, mỗi cạnh góc vuông bằng 

a) Cạnh huyền nhân với sin góc đối hoặc cosin góc kề.

b) Cạnh góc vuông kia nhân với tang góc đối hoặc cotang góc kề.

Các công thức trong tam giác vuông :

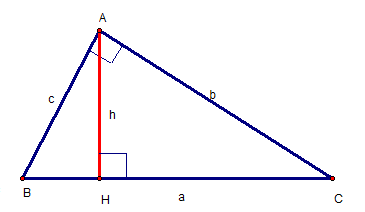
Cho ΔABC vuông tại A :

1. BC² = AC² + AB²
2. AB² = BC.BH; AC² = BC.CH
3. AH² = HB.HC
4. BC.AH = AB.AC
5. 
6. AC = BC.sin B = BC.cos C = AB.tan B = AB.cotg C.
7. AB = BC.sin C = BC.cos B  = AC. tan C = AC.cotg B

Định lí hàm cos : BC² = AC² + AB² – 2AB.AC.cosA

Công thức :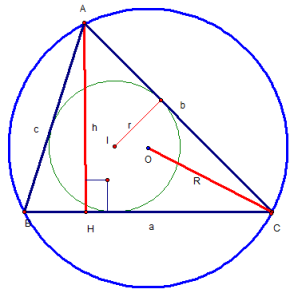

• a² = b² + c² – 2bccosA.
• b² = a² + c² – 2accosB.
• c² = b² + a² – 2abcosC.

Hệ quả : (tính góc tam giác )

Công thức tính đường trung tuyến :

Ví dụ áp dụng công thức trong tam giác vuông

=> Tham khảo bài viết chi tiết đầy đủ hệ thức lượng trong tam giác vuông